7. Sınıf Matematik Ders Kitabı 241-242-251. Sayfa Cevapları MEB Yayınları

7. Sınıf Matematik Ders Kitabı 241-242-251. Sayfa Cevapları MEB Yayınları 2023-2024 eğitim-öğretim yılı konusu içerisinde 7. sınıf öğrencilerinin en çok ihtiyaç duyabileceği konular arasında bulunan ve içerisinde Aritmetik Ortalama – Tepe Değer – Ortanca konusunun yer aldığı 7. Sınıf Matematik Ders Kitabı Sayfa 241-242-251 Cevapları konusunu paylaştık. Cevaplarla ilgili görüş ve önerilerinizi yorumlardan yazarak bildirebilirsiniz.

7. Sınıf MEB Yayınları Matematik Ders Kitabı 242-251. Sayfa Cevapları Aritmetik Ortalama – Tepe Değer – Ortanca

7. Sınıf Matematik Ders Kitabı Sayfa 241 Cevapları MEB Yayınları

Hazır Mıyız?

7-A sınıfı öğrencilerinden Zeynep ve Rümeysa’nın ilk dönem matematik sınavlarından aldıkları puanlar şu şekildedir:

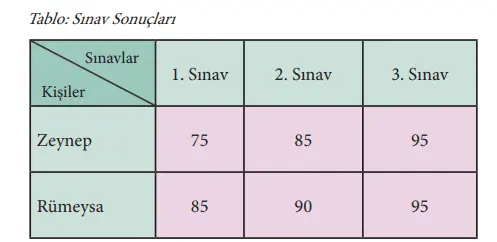
Yukarıdaki tabloda verilenlere göre aşağıdaki soruları cevaplandırınız.

1. Zeynep ve Rümeysa’nın aldıkları puanların aritmetik ortalamalarını ayrı ayrı hesaplayınız
Cevap: 

Zeynep → 75 + 85 + 95 = 255
                   255 ÷ 3 =85

Rümeysa → 85 + 90 + 95 = 270
                       270 ÷ 3 = 90

2. Zeynep ve Rümeysa’nın aldıkları puanların açıklıklarını ayrı ayrı hesaplayınız
Cevap:

 Zeynep → 95 – 75 = 20
Rümeysa → 95 – 85 = 10

3. Zeynep ve Rümeysa’nın başarı durumlarını karşılaştırınız.
Cevap: Rümeysa’nın aritmetik ortalamasına göre Zeynep’e göre daha başarılıdır.

7. Sınıf Matematik Ders Kitabı Sayfa 242 Cevapları MEB Yayınları

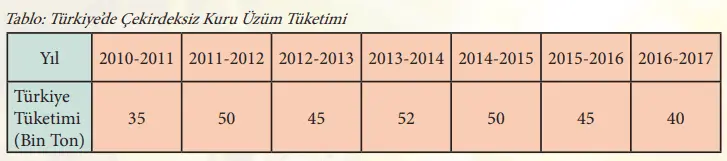
Yukarıdaki tabloda Türkiye’de tüketilen çekirdeksiz kuru üzüm miktarı verilmektedir. Tabloyu ve metinde verilen bilgileri dikkate alarak aşağıdaki soruları cevaplayınız.

➢ Türkiye’de yıllara göre ortalama kaç bin ton çekirdeksiz kuru üzüm tüketilmektedir?
Cevap:  

35 + 50 + 45 + 52 + 50 + 45 + 40 = 317
317 ÷ 7 = 45,29

➢ Tabloya göre tüketilen çekirdeksiz kuru üzüm miktarlarından en çok tekrar eden değer hangisidir?
Cevap: En çok tekrar eden değer 45 ve 50’dir. 

35 – 50 – 45 – 52 – 50 – 45 – 40 

➢ Tüketilen çekirdeksiz kuru üzüm verilerini küçükten büyüğe veya büyükten küçüğe sıraladığımızda ortadaki miktarın değişip değişmediğini nasıl yorumlarsınız?
Cevap: 

Küçükten büyüğe → 35 < 40 < 45 = 45 < 50 = 50 < 52
Büyükten küçüğe → 52 > 50 = 50 > 45 = 45 > 40 > 35 

Ortadaki miktar değişmemiştir. 

7. Sınıf Matematik Ders Kitabı Sayfa 251 Cevapları MEB Yayınları

SIRA SİZDE

1. Aşağıdaki boşluklara uygun ifadeleri yazınız.
Cevap:

a. Bir bütünün parçaları verilip bütün ile parçaları karşılaştırılmak isteniyorsa …..daire…. grafiği kullanılır.
b. Değerler gösterilirken ve veriler arasında karşılaştırma yapılırken …sütun… grafiği kullanılır.
c. Bir veri grubundaki verilerin belirli zaman aralığındaki değişimini (artış veya azalışını ) görmek için …çizgi… grafiği kullanılır.

2. 7-H sınıfında yapılan başkanlık seçiminde Zehra 7, Ece 9, Efe 8, Ahmet 6 oy almıştır. Bu verilere ait sıklık tablosunu doldurunuz. Tablodan yararlanarak daire ve sütun grafiklerini oluşturunuz.
Cevap: 

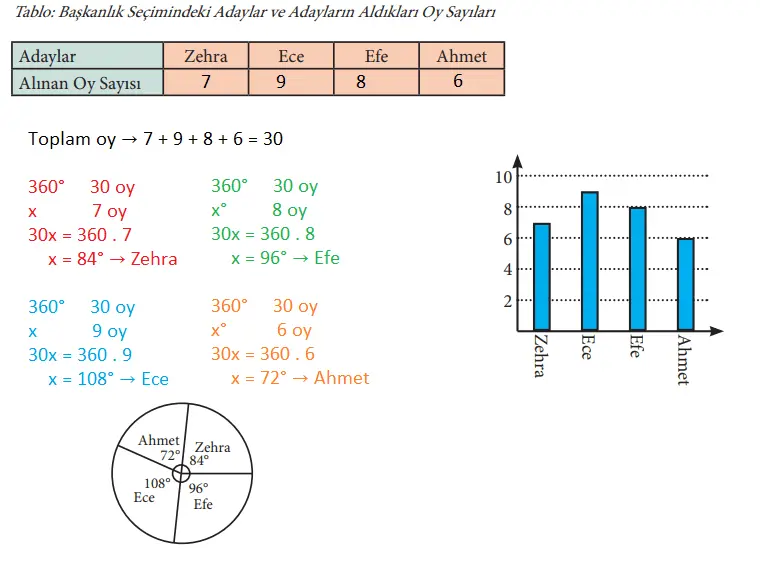
3. 4, 3, 8, 9, 14, 6, 4, 7, 9, 6 veri grubunun tepe değer, ortanca ve aritmetik ortalamasını bulunuz
Cevap: 

3, 4, 4, 6, 6, 7, 8, 9, 9, 14 

Tepe değer → 4, 6, 9
Ortanca → 6 + 7 = 13 → 13 ÷ 2 = 6,5 olur.
Aritmetik ortalama → 3 + 4 + 4 + 6 + 6 + 7 + 8 + 9 + 9 + 14 = 70
                                         70 ÷ 10 = 7 olur

4. Yaşlarının aritmetik ortalaması 35 olan 4 kişilik bir gruba 45 yaşında biri katılırsa yeni ortalama kaç olur?
Cevap: 

35 x 4 = 140
140 + 45 = 185
185 ÷ 5 = 37

5. Aşağıdaki ifadeleri inceleyiniz. İfadeler doğru ise “D”, yanlış ise “Y” yazınız
Cevap: 

a. (..Y..) Bir veri grubunda ortanca bulunurken verilerin sıralaması önemli değildir.
→ Küçükten büyüğe sıralanması gerekir. 

b. (..D..) Bir veri grubunun 4 tane tepe değeri olabilir.
c. (..Y..) Bir veri grubuna aritmetik ortalamadan daha büyük bir sayı eklenirse ortalama azalır.
→ Bir veri grubuna aritmetik ortalamadan daha büyük bir sayı eklenirse ortalama artar

ç. (..D..) Herhangi bir veri grubunun ortalaması, ortancası ve tepe değeri birbirine eşit olabilir.
d. (..D..) Veri adedi çift sayıda ise ortancayı bulmak için ortadaki iki sayının ortalaması alınır.
e. (..Y..) Bir veri grubunun her zaman tepe değeri mevcuttur.
→ Bir veri grubunun her zaman tepe değeri olmayabilir

f. (..Y..) Bir veri grubunda birden fazla ortanca bulunabilir
→ ortanca olan sayı çiftse toplanıp ikiye bölünür ve ortanca bulunur.