6. Sınıf Matematik Ders Kitabı 68-69-70-71-72-73-74-75. Sayfa Cevapları 1. KİTAP

6. Sınıf Matematik Ders Kitabı 68-69-70-71-72-73-74-75. Sayfa Cevapları 1. KİTAP 2025-2026 eğitim-öğretim yılı konusu içerisinde 6. sınıf öğrencilerinin en çok ihtiyaç duyabileceği konular arasında bulunan ve içerisinde İstatistik ve Araştırma Sorularında Sağlanması Gereken Ölçütler konusunun bulunduğu 6. Sınıf Matematik Ders Kitabı Sayfa 68-69-70-71-72-73-74-75 Cevapları konusunu paylaştık. Cevaplarla ilgili görüş ve önerilerinizi yorumlardan yazarak bildirebilirsiniz.
6.Sınıf MEB Yayınları Matematik Ders Kitabı 68-69-70-71-72-73-74-75. Sayfa Cevapları 1. KİTAP İstatistik ve Araştırma Sorularında Sağlanması Gereken Ölçütler
- 6. Sınıf Matematik Ders Kitabı Sayfa 68 Cevapları MEB Yayınları
- 6. Sınıf Matematik Ders Kitabı Sayfa 69 Cevapları MEB Yayınları
- 6. Sınıf Matematik Ders Kitabı Sayfa 70 Cevapları MEB Yayınları
- 6. Sınıf Matematik Ders Kitabı Sayfa 71 Cevapları MEB Yayınları
- 6. Sınıf Matematik Ders Kitabı Sayfa 72 Cevapları MEB Yayınları
- 6. Sınıf Matematik Ders Kitabı Sayfa 73 Cevapları MEB Yayınları
- 6. Sınıf Matematik Ders Kitabı Sayfa 74 Cevapları MEB Yayınları
- 6. Sınıf Matematik Ders Kitabı Sayfa 75 Cevapları MEB Yayınları
6. Sınıf Matematik Ders Kitabı Sayfa 68 Cevapları MEB Yayınları
Etkinlik 5 – Ölçütlere Uygun Araştırma Sorusu
Aşağıdaki örneği araştırma sorusunun sağlaması gereken ölçütlere göre inceleyelim.

Yukarıda verilen örneğe göre aşağıdaki soruların araştırma sorusu olup olmadıklarını inceleyerek nedenleriyle açıklayınız.
a) Bilge’nin kitaplığında kaç tane hikâye kitabı vardır?
Cevap: Bu bir araştırma sorusudur çünkü soruda Bilge’nin kitaplığında hikaye kitaplarının sayısını belirleme amacı taşınıyor. Kitaplar sayılarak veya listeden kontrol edilerek veri toplanabilir. Her kitap sayılabilir bir değerdedir ve kitap sayısı zamanla değişebileceğinden ötürü değişkenlik vardır.
b) Türkiye’de illere göre kayak merkezi sayısı kaçtır?
Cevap: Bu bir araştırma sorusudur çünkü Türkiye’deki illerin sahip olduğu kayak merkezinin belirlenmesi amaçlanmış. Kurumlardan bilgi alarak veri toplanabilir. Kayak merkezleri sayısal olarak belirlenebilir durumdadır. Kayak merkezleri açıldıkça veya kapandıkça sayı değiştiği için değişkenlikte vardır.
c) 6-A sınıfındaki öğrencilerin matematik dersinden bir haftada çözdüğü soru sayısı kaçtır?
Cevap: Bu bir araştırma sorusudur çünkü sınıftaki öğrencilerin bir haftada çözdüğü soru sayısı belirleme amacı taşınıyor. Öğrencilere sorularak veya öğretmene danışılarak veri toplanabilir durumdadır. Her öğrencinin çözdüğü sayı belirlenebilir durumdadır ve öğrencilerin çözdüğü sayı farklı olabileceği için değişkenlikte vardır.
ç) İzmir’in nüfusu en fazla olan ilçesi hangisidir?
Cevap: Bu bir araştırma sorusu değildir. Veri toplanabilse bile amaç “en fazla olan ilçeyi belirlemek” olduğu için araştırma sorusundan çok bilgi sorusudur. Değişkenlik içermez.
6. Sınıf Matematik Ders Kitabı Sayfa 69 Cevapları MEB Yayınları
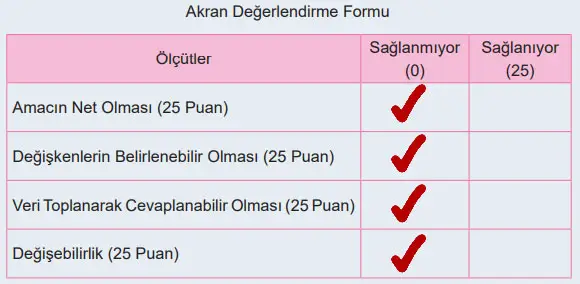
Etkinlik 6: Arkadaşımızı Değerlendirelim
Değerlendiren Öğrencinin Adı ve Soyadı: Mehmet Aslan
Akran Değerlendirmesi Yapılan Öğrencinin Adı ve Soyadı: Gökçe Yıldırım
Etkinlik/Çalışma: Sınıfımızdaki öğrencilerin bir ayda okuduğu kitap sayısı araştırması
Değerlendirme Tarihi: 15/10/2025
Yönerge: Öğretmeninizle belirlediğiniz bir konu hakkında araştırma sorusu oluşturunuz. Daha sonra her birinizin oluşturduğu araştırma sorusunu aşağıdaki ölçütlere uygun olarak değerlendiriniz
Oluşturulan Araştırma Sorusu: Atatürk Ortaokulu’nda en sevilen dersler nelerdir?
Değerlendirilen Akrana Verilen Puan (100 puan üzerinden): 100 puan
Yorumlar ve Öneriler: Arkadaşım sorularını daha geniş tutarak araştırmayı daha eğlenceli hale getirebilir.
6. Sınıf Matematik Ders Kitabı Sayfa 70 Cevapları MEB Yayınları
Etkinlik 7: Temiz Çevre, Kazanılan Gelecek
Bu duruma yönelik araştırma soruları belirleyiniz. Belirlediğiniz araştırma sorularınızı arkadaşlarınızla paylaşarak tartışınız.
Cevap:
- Evimizde günlük ne kadar plastik kullanıyoruz?
- Plastik kullanımını azaltmak için hangi yöntemleri uygulayabiliriz?
Etkinlik 8: Gerçek Yaşam Problemlerine Uygun Araştırma Soruları
Günlük hayatınızda karşılaştığınız bir problem belirleyiniz ve bu problemin çözümü için araştırma soruları oluşturunuz. Araştırma sorularınızı oluştururken bir araştırma sorusunun sağlaması gereken ölçütleri dikkate alınız.
1) Belirlediğiniz problem: Evde çöplerin geri dönüşüme uygun şekilde ayrılmaması ve çöp miktarının fazla olması.
2) Problemin çözümü için hazırladığınız araştırma soruları:
- Evimizde bir günde ne kadar çöp oluşur?
- Evimizdeki çöplerin ne kadarı geri dönüşüme uygun plastik, cam, kağıt, veya metal atıklardan oluşuyor?
- Çözümlerden hangileri çöp miktarının azaltılmasına yol açabilir?
6. Sınıf Matematik Ders Kitabı Sayfa 71 Cevapları MEB Yayınları
Etkinlik 1: Kitap Okuma Sürelerini Araştırıyorum

6-A sınıfındaki öğrencilerin günlük ortalama kitap okuma sürelerini dakika cinsinden belirlemeniz istenmektedir.
Bu araştırmanın planlama sürecine yönelik aşağıdaki soruları cevaplayınız.
a) Araştırmanın amacı nedir?
Cevap: 6-A sınıfındaki öğrencilerin günlük ortalama kitap okuma sürelerini dakika olarak belirlemek.
b) Bu araştırmaya uygun olarak oluşturulabilecek araştırma sorusu ne olabilir? Arkadaşlarınızla paylaşarak tartışınız.
Cevap: 6-A sınıfındaki öğrenciler günlük ortalama kaç dakika kitap okumaktadır?
c) Verileri nereden toplarsınız? Hedef kitlenizi yazınız.
Cevap: 6-A sınıfındaki öğrencilerden toplanır.
ç) Hangi veri toplama araçlarını kullanırsınız?
Cevap: Verileri anket düzenleyerek, gözlem yaparak ve okuma çizelgesinden toplayabiliriz.
d) Bu araştırma için veri toplama sürecine ne kadar zaman ayırmalısınız?
Cevap: Veriyi toplamak için 2 hafta yada 1 ay yeterli olabilir.
e) Topladığınız verileri kaydetmek ve görselleştirmek için hangi araçları tercih edersiniz? (dijital araç gereçler, not defteri vb.)
Cevap: Dijital araçlar, not defteri, tablo çizelgeleri ve görselleştirme amaçlı grafikler kullanılabilir.
f) Oluşturduğunuz araştırma planını sınıf arkadaşlarınızla paylaşarak onların araştırma planları ile karşılaştırınız. Planınızın güçlü ve zayıf yönlerini arkadaşlarınızla tartışınız.
Cevap:
Güçlü Yönler: Amaç gerçek veriyi toplamak, veri görselleştirme planı hazır.
Zayıf Yönler: Verilerin doğruluğu yalnızca öğrencilerin dürüstlüğüne kalmış. Doğrulanabilir sayılmaz.
6. Sınıf Matematik Ders Kitabı Sayfa 72 Cevapları MEB Yayınları
Etkinlik 2: Genç Nüfusu Araştırıyorum
15-24 yaş grubundaki kişiler “genç nüfus” olarak adlandırılmaktadır. Genç nüfus grubundaki kişi sayısını belirlemek amacıyla aşağıdaki araştırma sorusu oluşturulmuştur.

Araştırma sorusu: “2023 yılında genç nüfus grubundaki kişi sayısı kaçtır?”
Bu araştırmayla ilgili veri toplama sürecine yönelik aşağıdaki soruları cevaplayınız.
a) Çevrenizde bulunan genç nüfus grubundaki kişi sayısını belirlemek için verileri kimlerden toplarsınız? Hedef kitleniz kimler olur?
Cevap: Verileri çevremizden, arkadaşlardan, komşularımızdan veya okuldaki diğer öğrencilerden bulabiliriz. Hedef kitlemiz 15-25 yaş arasındaki insanlar olabilir.
b) İlinizde bulunan genç nüfus grubundaki kişi sayısını belirlemek için verileri kimlerden toplarsınız? Hedef kitleniz kimler olur?
Cevap: İl nüfus müdürlüğü kayıtları, belediye istatistikleri ve TÜİK verilerinden yararlanabiliriz. Çevremizdeki 15-25 yaş arasındaki insanlar hedef kitlemizdir.
c) Türkiye’nin genç nüfus grubundaki kişi sayısını belirlemek için verileri kimlerden toplarsınız? Hedef kitleniz kimler olur?
Cevap: Verileri Çalışma ve Sosyal Politikalar Bakanlığından ve TÜİK’ten bulabiliriz. Hedef kitlemiz yine 15-25 yaş arasındaki insanlardır.
6. Sınıf Matematik Ders Kitabı Sayfa 73 Cevapları MEB Yayınları
Etkinlik 1 – Sağlıklı Yaşam
Araştırma Sorusu: İnsanların sağlıklı yaşamı destekleyen alışkanlıkları hangi sıklıkla uygulanmaktadır?
SAĞLIKLI YAŞAMI DESTEKLEYEN ALIŞKANLIKLAR İLE İLGİLİ ANKET
Katılımcının
Adı ve Soyadı: Kamil Ak
Yaşı: 37
Cinsiyeti: Erkek
Mesleği: Marangoz

6. Sınıf Matematik Ders Kitabı Sayfa 74 Cevapları MEB Yayınları
Etkinlik 2: Dijital Hizmetler

Buna göre aşağıdaki soruları cevaplayınız.
a) Dijital ortamlarda kişisel verilerin gizlilik ihlalleri ve olası sonuçlarını yazıp arkadaşlarınızla tartışınız.
Cevap: Kişisel verilerin ihlal edilmesi insanların maddi kayıplar elde etmesi, gizli tuttuğu özel bilgilerinin ifşa olarak rencide olmalarına sebep olabilir.
b) “Bireylerin E-Devlet platformunda işlem yaparken kişisel verilerini koruma konusundaki farkındalık düzeyi nedir?” araştırma sorusuna uygun anket soruları oluşturunuz.
Cevap:
- E-Devlet şifrenizi kimseyle paylaşıyor musunuz?
- E-Devlet işlemlerinde güçlü bir şifre kullanıyor musunuz?
- Kişisel bilgilerinizi dijital ortamda paylaşırken dikkatli misiniz?
- E-Devlet’teki gizlilik önlemlerinden haberdar mısınız?
c) Oluşturduğunuz anket sorularını çevrenizdeki bireylere uygulayıp topladığınız verileri aşağıdaki alana kaydediniz. Elde ettiğiniz sonuçları arkadaşlarınızla tartışınız. Ayrıca verilerini topladığınız bireylerin kişisel bilgilerinin gizlilik ve mahremiyetine dikkat etmeyi unutmayınız.
Cevap: Çevremdeki 15 kişiye oluşturduğum soruları sordum ve şu cevapları aldım:
- “E-Devlet şifrenizi kimseyle paylaşıyor musunuz?” sorusuna 12 kişi evet, 3 kişi hayır cevabını verdi.
- “E-Devlet işlemlerinde güçlü bir şifre kullanıyor musunuz?” sorusuna 5 kişi evet, 10 kişi hayır cevabını verdi.
- “Kişisel bilgilerinizi dijital ortamda paylaşırken dikkatli misiniz?” sorusuna 15 kişi evet yanıtını verdi.
- “E-Devlet’teki gizlilik önlemlerinden haberdar mısınız?” sorusuna 2 kişi evet, 13 kişi hayır yanıtını verdi.
6. Sınıf Matematik Ders Kitabı Sayfa 75 Cevapları MEB Yayınları
Etkinlik 3: Anket Formu Hazırlıyorum
Belirleyeceğiniz bir konuyla ilgili araştırma sorusu ve bu araştırma sorusuna uygun anket soruları oluşturarak veri toplayınız. Anket sorularını hazırlarken soruların taşıması gereken özellikleri dikkate alınız. Sınıfta gruplar oluşturup iş birliği ile bu süreci yürütünüz.
Araştırma Sorusu: 6-A sınıfındaki öğrenciler 1 haftada kaç gün kahvaltı yapmaktadır?
ANKET
Aradığınız ödevi bulamadıysanız lütfen MEB Yayınları 2025 ana içeriğimizi ziyaret ediniz.
Ders ve Çalışma kitabı cevapları aramalarınızda internet sitemizi daha üst sıralarda listelemek için aramalarınızın sonuna "forum sınıf" yazabilirsiniz.
Örnek Kullanım: 3. sınıf türkçe sayfa 11 forum sınıf

