7. Sınıf Matematik Ders Kitabı Cevapları MEB Yayınları 2025
7.Sınıf Matematik Ders Kitabı Cevapları MEB Yayınları 2025-2026 Eğitim-Öğretim yılı içerisinde ortaokul öğrencilerinin en çok arattıkları içeriklerden birisi olan 7. Sınıf Matematik Ders Kitabı Cevapları MEB Yayınları konusunun tüm cevaplarını bu konu altında paylaşmış bulunuyoruz. Öğrencilerimiz konu içerisinde eksik veya hatalı bir kısım ile karşılaşmaları halinde bu durumu bizlere yorumlar bölümünden yazarak bildirebilirler. Öğrencilerimizin hata bildirimi içeren yorumları sitemizin uzman yöneticileri tarafından denetlenmek ve incelemek amacıyla sıraya alınmaktadır.

7. sınıf matematik ders kitabı cevapları konusunda 7. sınıf öğrencilerimize hitap eden bir matematik kitabının cevapları paylaşılmıştır. Öğrencilerimiz 2025-2026 Eğitim-Öğretim hayatı dünya genelinde ortaya çıkan koronavirüs hastalığı ile bir süre internet üzerinden online olarak yapılmıştı. Bu süreç içerisinde öğrencilerin en çok zorlandıkları ders matematik dersidir. Özellikle 7. sınıf öğrencilerinin internet üzerinde en çok arattıkları başlık 7. Sınıf Matematik Ders Kitabı cevapları Meb yayınları olmuştur. Çünkü kendi çabaları dahilinde çalışan öğrenciler cevaplarını ancak internet üzerinden kontrol ederek öğrenebilmektedirler. Durum böyle olunca bizlerde onlar için cevap anahtarlarını internet üzerinden yayınladık ve öğrencilerimizin kendi eksiklerini, yanlışlarını ve hatalı oldukları konuları görmelerini sağlamaya çalıştık. Bu zorlu dönemde birçok yayında 7. Sınıf Matematik Ders Kitabı cevaplarını bize verdiler ve sitemiz bünyesinde bunları da öğrencilerimiz ile paylaştık. Matematik ders kitabı cevapları aratırken hangi yayın ve kaçıncı sınıf olduğu ile ilgili bilgileri girerek aratmak sizi istediğiniz cevaba götürmekte kolaylık sağlayacaktır. Aynı zamanda aradığınız cevabı daha kolay bulabilmek için sayfa ve soru numarasını da girebilirsiniz.

7 Sınıf Matematik Ders Kitabı her düzeydeki öğrenci için çok önemli ve iyi bilinmesi gereken bir derstir. Öğrenciler yaptıkları yanlışların üzerine giderek bunları düzeltmeli ve seviyelerini ilerletmelidirler. Bizim yayınladığımız cevaplar ise düzeltme işi için büyük önem taşır. Çünkü öğrenci yaptığı yanlışı bu sayede görmektedir ve farkında varmaktadır. Bu ders için her ne kadar sınav soru tarzına yakın olan MEB yayınları olsa dahi öğrencilerimiz farklı farklı kaynaklarının olması da onların yararına olacaktır. 7. sınıf Matematik ders kitabı her 7. sınıf öğrencisi için zordur ve bunun üstesinden gelmeye çalışmaktadırlar. İnternetten baktıkları cevaplarda çıkan yanlış soruların üstüne gitmedikten sonra zor olmaya devam edebilir. Ancak cevaplarımızın üstüne gidip uğraşırsak eğer zor değil aksine en sevdiğimiz ders bile olabilir.
7.Sınıf Matematik Dersi Cevapları MEB Yayınları ile ilgili herhangi bir şikayet çıkar ise bunu forum sitemizin dilek istek şikayet kısmından şikayet başlığı altında soru ve sayfa numarası ile yazıp attığınız takdirde editör arkadaşlarımız sorununuzu en kısa zamanda çözmek için çaba sarf eder. Bu çaba sonucu yanlışlık giderilir ve sayfamızı güncelleyerek sizlere en iyi şekilde hizmet vermekten gurur duyarız.
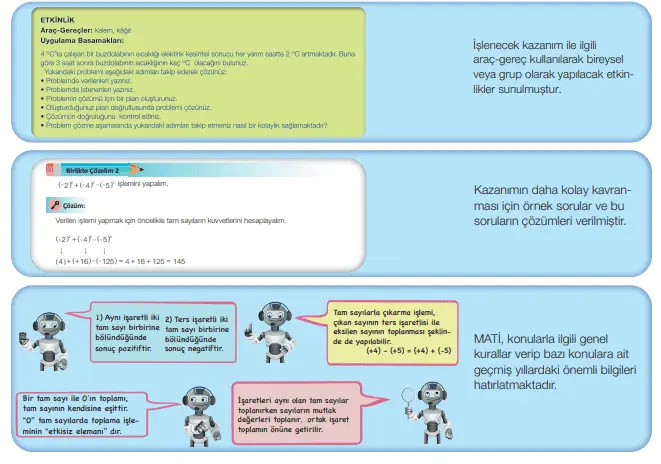
Öğrencilerimizde bu durumun gözlemlenmemesi için öğrencilerimize eskisine göre artık daha çok ders çalışmalarını tavsiye ediyoruz. Ders kitaplarındaki etkinlikleri, soruları ve problemleri çözmelidir. Takıldıkları yerleri veya yaptığı çalışmaları kontrol etmek için internette arama yaparak forumsinif.com daki 7. sınıf matematik ders kitabı cevapları konularını ziyaret edebilirler. Böylece konumuzdaki cevaplarla kendi cevaplarını karşılaştırıp hatalarını gözlemleyebilirler.
7.Sınıf Matematik Ders Kitabı Cevapları MEB Yayınları
7. Sınıf Matematik Ders Kitabı Cevapları MEB Yayınları 2025-2026 Eğitim-Öğretim yılı konusu içerisinde 7. sınıf öğrencilerimizin ihtiyaç duyabilecekleri konular arasında bulunan 7. sınıf matematik ders kitabı MEB yayınları sayfa 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26 ,27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40 ,41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60,61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 266’nın cevapları aşağıda bulunan bağlantılar bölmesinde yayınlanmıştır. Cevabını görmek istediğiniz sayfa numarasını veya etkinlik ismini aşağıdan bularak üzerine tıklamanız yeteri olacaktır. Böylece cevabını görmek istediğiniz sayfaya veya etkinliğe otomatik olarak yönlendirilmiş olacaksınız. 7. Sınıf Matematik Ders Kitabı Cevapları konusunda eksik veya hatayla karşılaşmanız durumunda bize bu durumu yorumlar bölümünden yazarak bildirebilirsiniz.
1. Ünite – Sayılar ve İşlemler
1. Bölüm: Tam Sayılarla İşlemler
Hazır Mıyız Etkinliği Sayfa 12 Cevapları
Tam Sayılarla Toplama ve Çıkarma Etkinliği Sayfa 13-14-15-16-17-18-19 Cevapları
Kazanım Kavrama Testi – 1 Etkinliği Sayfa 20 Cevapları
Tam Sayılarla Çarpma ve Bölme Etkinliği Sayfa 21-22-23-24-25-26-27-28-29 Cevapları
Kazanım Kavrama Testi – 2 Etkinliği Sayfa 30 Cevapları
Tam Sayıların Tekrarlı Çarpımları Etkinliği Sayfa 31-32 Cevapları
Kazanım Kavrama Testi – 3 Etkinliği Sayfa 33 Cevapları
Tam Sayı Problemleri Etkinliği Sayfa 34-35 Cevapları
1. Ünite Değerlendirme – 1 Etkinliği Sayfa 36-37 Cevapları
Beceri Temelli Sorular – 1 Etkinliği Sayfa 38-39-40 Cevapları
2. Ünite – Sayılar ve İşlemler
1. Bölüm: Rasyonel Sayılar
Hazır Mıyız Etkinliği Sayfa 42 Cevapları
Rasyonel Sayılar Etkinliği Sayfa 43-44-45-46 Cevapları
Rasyonel Sayıların Ondalık Gösterimi Etkinliği Sayfa 47-48-49-50 Cevapları
Kazanım Kavrama Testi – 4 Etkinliği Sayfa 51 Cevapları
Rasyonel Sayıları Sıralama Etkinliği Sayfa 52-53-54-55-56 Cevapları
Kazanım Kavrama Testi – 5 Etkinliği Sayfa 57 Cevapları
2. Bölüm: Rasyonel Sayılarla İşlemler
Hazır Mıyız Etkinliği Sayfa 58 Cevapları
Rasyonel Sayılarla Toplama ve Çıkarma Etkinliği Sayfa 59-60-61-62-63-64-65 Cevapları
Kazanım Kavrama Testi – 6 Etkinliği Sayfa 66 Cevapları
Rasyonel Sayılarla Çarpma ve Bölme İşlemi Etkinliği Sayfa 67-68 Cevapları
Rasyonel Sayılarla Çarpma İşlemi Etkinliği Sayfa 69-70-71-72 Cevapları
Rasyonel Sayılarla Bölme İşlemi Etkinliği Sayfa 73-74-75 Cevapları
Kazanım Kavrama Testi – 7 Etkinliği Sayfa 76 Cevapları
Rasyonel Sayılarla Çok Adımlı İşlemler Etkinliği Sayfa 77-78-79-80 Cevapları
Rasyonel Sayıların Kare ve Küpleri Etkinliği Sayfa 81-82-83 Cevapları
Kazanım Kavrama Testi – 8 Etkinliği Sayfa 84 Cevapları
Rasyonel Sayı Problemleri Etkinliği Sayfa 85-86-87-88 Cevapları
Kazanım Kavrama Testi – 9 Etkinliği Sayfa 89 Cevapları
2.Ünite Değerlendirme – 2 Etkinliği Sayfa 90-91 Cevapları
Beceri Temelli Sorular – 2 Etkinliği Sayfa 92-93-94 Cevapları
3. Ünite – Cebir
1. Bölüm: Cebirsel İfadeler
Hazır Mıyız Etkinliği Sayfa 96 Cevapları
Cebirsel İfadelerle Toplama, Çıkarma ve Çarpma Etkinliği Sayfa 97-98-99-100 Cevapları
Sayı Örüntüleri Etkinliği Sayfa 101-102-103-104 Cevapları
Kazanım Kavrama Testi – 10 Etkinliği Sayfa 105 Cevapları
2. Bölüm: Eşitlik ve Denklem
Eşitlik ve Denklem Etkinliği Sayfa 106-107-108-109-110-111 Cevapları
Kazanım Kavrama Testi – 11 Etkinliği Sayfa 112 Cevapları
3. Ünite Değerlendirme – 3 Etkinliği Sayfa 113 Cevapları
Beceri Temelli Sorular – 3 Etkinliği Sayfa 114-115-116-117-118 Cevapları
4. Ünite – Sayılar ve İşlemler
1. Bölüm: Oran ve Orantı
Hazır Mıyız Etkinliği Sayfa 120 Cevapları
Oran Etkinliği Sayfa 121-122-123-124 Cevapları
Orantı Etkinliği Sayfa 125-126-127-128 Cevapları
Doğru Orantı – Ters Orantı Etkinliği Sayfa 129-130-131-132-133-134-135 Cevapları
Kazanım Kavrama Testi – 12 Etkinliği Sayfa 136 Cevapları
2. Bölüm: Yüzdeler Cevapları
Hazır Mıyız Etkinliği Sayfa 137 Cevapları
Yüzdeler Etkinliği Sayfa 138-139-140-141-142 Cevapları
Kazanım Kavrama Testi – 13 Etkinliği Sayfa 143 Cevapları
4. Ünite Değerlendirme – 4 Etkinliği Sayfa 144-145 Cevapları
Beceri Temelli Sorular – 4 Etkinliği Sayfa 146-147-148 Cevapları
5. Ünite – Geometri ve Ölçme
1. Bölüm: Doğrular ve Açılar
Hazır Mıyız Etkinliği Sayfa 150 Cevapları
Doğrular ve Açılar Etkinliği Sayfa 151-152-153-154 Cevapları
Kazanım Kavrama Testi – 14 Etkinliği Sayfa 155 Cevapları
Üç Doğrunun Düzlemde Birbirlerine Göre Durumları Etkinliği Sayfa 156-157-158-159-160-161-162-163 Cevapları
Kazanım Kavrama Testi – 15 Etkinliği Sayfa 164 Cevapları
2. Bölüm: Çokgenler
Hazır Mıyız Etkinliği Sayfa 165 Cevapları
Çokgenler Etkinliği Sayfa 166-167-168-169-170-171-172 Cevapları
Düzgün Çokgenler Etkinliği Sayfa 173-174-175-176-177 Cevapları
Dörtgenler Etkinliği Sayfa 178-179-180-181-182-183-184-185-186-187-188-189 Cevapları
Alan Problemleri Etkinliği Sayfa 190-191-192-193-194-195-196-197-198-199 Cevapları
Kazanım Kavrama Testi – 16 Etkinliği Sayfa 200 Cevapları
3. Bölüm: Çember ve Daire
Hazır Mıyız Etkinliği Sayfa 201 Cevapları
Çemberde Açılar Etkinliği Sayfa 202-203-204-205-206-207 Cevapları
Kazanım Kavrama Testi – 17 Etkinliği Sayfa 208 Cevapları
Çember ve Çember Parçasının Uzunluğu Etkinliği Sayfa 209-210-211-212-213-214 Cevapları
Kazanım Kavrama Testi – 18 Etkinliği Sayfa 215 Cevapları
Dairenin Alanı Etkinliği Sayfa 216-217-218-219-220 Cevapları
Kazanım Kavrama Testi – 19 Etkinliği Sayfa 221 Cevapları
5. Ünite Değerlendirme – 5 Etkinliği Sayfa 222-223 Cevapları
Beceri Temelli Sorular – 5 Etkinliği Sayfa 224-225-226-227-228 Cevapları
6. Ünite – Veri İşleme ve Yapı Görünümleri
1. Bölüm: Veri Analizi
Hazır Mıyız Etkinliği Sayfa 230 Cevapları
Daire Grafiği Etkinliği Sayfa 231-232-233-234 Cevapları
Çizgi Grafiği Etkinliği Sayfa 235-236-237-238-239 Cevapları
Kazanım Kavrama Testi – 20 Etkinliği Sayfa 240 Cevapları
Aritmetik Ortalama-tepe Değer-Ortanca Etkinliği Sayfa 241-242-243-244-245-246-247-248-249-250-251 Cevapları
Kazanım Kavrama Testi – 21 Etkinliği Sayfa 252 Cevapları
2. Bölüm: Cisimlerin Farklı Yönlerden Görünümleri
Hazır Mıyız Etkinliği Sayfa 253 Cevapları
Cisimlerin Farklı Yönlerden Görünümleri Etkinliği Sayfa 254-255-256-257-258-259-260 Cevapları
Kazanım Kavrama Testi – 22 Etkinliği Sayfa 261 Cevapları
6. Ünite Değerlendirme – 6 Etkinliği Sayfa 262-263 Cevapları
Beceri Temelli Sorular – 6 Etkinliği Sayfa 264-265-266 Cevapları
7. Sınıf Matematik Ders Kitabı Cevapları MEB Yayınları
Aradığınız ödevi bulamadıysanız lütfen Edat Yayıncılık 2025 ana içeriğimizi ziyaret ediniz.
Ders ve Çalışma kitabı cevapları aramalarınızda internet sitemizi daha üst sıralarda listelemek için aramalarınızın sonuna "forum sınıf" yazabilirsiniz.
Örnek Kullanım: 3. sınıf türkçe sayfa 11 forum sınıf


